Portal:Mathematics

Abacus, a ancient hand-operated calculating.
Portrait of Emmy Noether, around 1900.
Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

Image 1

A stamp of Zhang Heng issued by China Post in 1955

Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.

Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
Image 2
In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.

The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)
Image 3

Cantor, c. 1910

Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.

Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
Image 4
The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group $S̃ 3$

The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers ( $..., -2, -1, 0, 1, 2, ...$ ) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.

A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
Image 5

Bust of Shen at the Beijing Ancient Observatory

Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).

In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
Image 6
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 7

Archimedes Thoughtful by Fetti (1620)

Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is considered one of the leading scientists in classical antiquity. Regarded as the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.

Archimedes' other mathematical achievements include deriving an approximation of pi ( $π$ ), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. In astronomy, he made measurements of the apparent diameter of the Sun and the size of the universe. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
Image 8

Noether c. 1900–1910

Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
$Image 9 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 9
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, $21$ is the GCD of $252$ and $105$ (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number $21$ is also the GCD of $105$ and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
Image 10
The number π (/paɪ/ ; spelled out as "pi") is a mathematical constant, approximately equal to 3.14159, that is the ratio of a circle's circumference to its diameter. It appears in many formulae across mathematics and physics, and some of these formulae are commonly used for defining π, to avoid relying on the definition of the length of a curve.

The number π is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as 22 7 {\displaystyle {\tfrac {22}{7}}} are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an algebraic equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. (Full article...)
Image 11
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 12

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 13

Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.

Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
Image 14

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 15

Portrait by Jakob Emanuel Handmann, 1753

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.

Euler is credited for popularizing the Greek letter π {\displaystyle \pi } (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation f ( x ) {\displaystyle f(x)} for the value of a function, the letter i {\displaystyle i} to express the imaginary unit − 1 {\displaystyle {\sqrt {-1}}} , the Greek letter Σ {\displaystyle \Sigma } (capital sigma) to express summations, the Greek letter Δ {\displaystyle \Delta } (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant e {\displaystyle e} , the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)

Good articles

Image 1

Portrait photograph of Alan Turing, taken on 29 March 1951.

Alan Mathison Turing (/ˈtjʊərɪŋ/; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist. He was highly influential in the development of theoretical computer science, providing a formalisation of the concepts of algorithm and computation with the Turing machine, which can be considered a model of a general-purpose computer. Turing is widely considered to be the father of theoretical computer science.

Born in London, Turing was raised in southern England. He graduated from King's College, Cambridge, and in 1938, earned a doctorate degree from Princeton University. During World War II, Turing worked for the Government Code and Cypher School at Bletchley Park, Britain's codebreaking centre that produced Ultra intelligence. He led Hut 8, the section responsible for German naval cryptanalysis. Turing devised techniques for speeding the breaking of German ciphers, including improvements to the pre-war Polish bomba method, an electromechanical machine that could find settings for the Enigma machine. He played a crucial role in cracking intercepted messages that enabled the Allies to defeat the Axis powers in many engagements, including the Battle of the Atlantic. (Full article...)
Image 2
Numbers written with Cistercian numerals. From left to right: 1 in units place, 2 in tens place (20), 3 in hundreds place (300), 4 in thousands place (4,000), then compound numbers 5,555, 6,789, 9,394.

The medieval Cistercian numerals, or "ciphers" in nineteenth-century parlance, were developed by the Cistercian monastic order in the early thirteenth century at about the time that Arabic numerals were introduced to northwestern Europe. They are more compact than Arabic or Roman numerals, with a single glyph able to indicate any integer from 1 to 9,999.

Digits are based on a horizontal or vertical stave, with the position of the digit on the stave indicating its place value (units, tens, hundreds or thousands). These digits are compounded on a single stave to indicate more complex numbers. The Cistercians eventually abandoned the system in favor of the Arabic numerals, but marginal use outside the order continued until the early twentieth century. (Full article...)
Image 3
Sunday Osarumwense Iyahen (3 October 1937 – 28 January 2018) was a Nigerian mathematician and politician, recognised for his contributions to the field of topological vector spaces and his service as a senator representing Bendel Central Senatorial District. Born in Benin City, Edo State, Nigeria, Iyahen was the eldest of at least seventeen children and embarked on an academic journey that led him to earn a first-class honours degree in mathematics from the University of Ibadan and later a Ph.D. and D.Sc. from the University of Keele.

Iyahen's academic career was marked by his tenure as a professor of mathematics at several universities in Nigeria and abroad. He served as the Head of the Department of Mathematics and Dean of the Faculty of Science at the University of Ibadan before joining the Institute of Technology, Benin (now known as the University of Benin), where he became the founding dean of the Faculty of Physical Sciences. His scholarly work includes over 100 published papers and contributions as editor-in-chief for mathematical journals. He was honoured with fellowships from the Nigerian Academy of Science and the Mathematical Association of Nigeria. As a politician, he was elected as a senator, where he contributed to national policy and development. (Full article...)
Image 4

Wigner in 1963

Eugene Paul Wigner (Hungarian: Wigner Jenő Pál, pronounced [ˈviɡnɛr ˈjɛnøː ˈpaːl]; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his contributions to the theory of the atomic nucleus and the elementary particles, particularly through the discovery and application of fundamental symmetry principles".

A graduate of the Technical Hochschule Berlin (now Technische Universität Berlin), Wigner worked as an assistant to Karl Weissenberg and Richard Becker at the Kaiser Wilhelm Institute in Berlin, and David Hilbert at the University of Göttingen. Wigner and Hermann Weyl were responsible for introducing group theory into physics, particularly the theory of symmetry in physics. Along the way he performed ground-breaking work in pure mathematics, in which he authored a number of mathematical theorems. In particular, Wigner's theorem is a cornerstone in the mathematical formulation of quantum mechanics. He is also known for his research into the structure of the atomic nucleus. In 1930, Princeton University recruited Wigner, along with John von Neumann, and he moved to the United States, where he obtained citizenship in 1937. (Full article...)
$Image 5 Dyadic rationals in the interval from 0 to 1 In mathematics, a dyadic rational or binary rational is a number that can be expressed as a fraction whose denominator is a power of two. For example, 1/2, 3/2, and 3/8 are dyadic rationals, but 1/3 is not. These numbers are important in computer science because they are the only ones with finite binary representations. Dyadic rationals also have applications in weights and measures, musical time signatures, and early mathematics education. They can accurately approximate any real number. The sum, difference, or product of any two dyadic rational numbers is another dyadic rational number, given by a simple formula. However, division of one dyadic rational number by another does not always produce a dyadic rational result. Mathematically, this means that the dyadic rational numbers form a ring, lying between the ring of integers and the field of rational numbers. This ring may be denoted '"`UNIQ--postMath-0000000B-QINU`"'. (Full article...)$

Image 5
Dyadic rationals in the interval from 0 to 1

In mathematics, a dyadic rational or binary rational is a number that can be expressed as a fraction whose denominator is a power of two. For example, 1/2, 3/2, and 3/8 are dyadic rationals, but 1/3 is not. These numbers are important in computer science because they are the only ones with finite binary representations. Dyadic rationals also have applications in weights and measures, musical time signatures, and early mathematics education. They can accurately approximate any real number.

The sum, difference, or product of any two dyadic rational numbers is another dyadic rational number, given by a simple formula. However, division of one dyadic rational number by another does not always produce a dyadic rational result. Mathematically, this means that the dyadic rational numbers form a ring, lying between the ring of integers and the field of rational numbers. This ring may be denoted $\mathbb {Z} [{\tfrac {1}{2}}]$ . (Full article...)
$Image 6 Natural patterns form as wind blows sand in the dunes of the Namib Desert. The crescent shaped dunes and the ripples on their surfaces repeat wherever there are suitable conditions. Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time. In the 19th century, the Belgian physicist Joseph Plateau examined soap films, leading him to formulate the concept of a minimal surface. The German biologist and artist Ernst Haeckel painted hundreds of marine organisms to emphasise their symmetry. Scottish biologist D'Arcy Thompson pioneered the study of growth patterns in both plants and animals, showing that simple equations could explain spiral growth. In the 20th century, the British mathematician Alan Turing predicted mechanisms of morphogenesis which give rise to patterns of spots and stripes. The Hungarian biologist Aristid Lindenmayer and the French American mathematician Benoît Mandelbrot showed how the mathematics of fractals could create plant growth patterns. (Full article...)$

Image 6
Natural patterns form as wind blows sand in the dunes of the Namib Desert. The crescent shaped dunes and the ripples on their surfaces repeat wherever there are suitable conditions.

Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.

In the 19th century, the Belgian physicist Joseph Plateau examined soap films, leading him to formulate the concept of a minimal surface. The German biologist and artist Ernst Haeckel painted hundreds of marine organisms to emphasise their symmetry. Scottish biologist D'Arcy Thompson pioneered the study of growth patterns in both plants and animals, showing that simple equations could explain spiral growth. In the 20th century, the British mathematician Alan Turing predicted mechanisms of morphogenesis which give rise to patterns of spots and stripes. The Hungarian biologist Aristid Lindenmayer and the French American mathematician Benoît Mandelbrot showed how the mathematics of fractals could create plant growth patterns. (Full article...)
Image 7

1963 statue of Anania Shirakatsi holding a globe at the entrance of the Matenadaran

Anania Shirakatsi (Old Armenian: Անանիա Շիրակացի, Anania Širakac’i, anglicized: Ananias of Shirak) was a 7th-century Armenian polymath and natural philosopher, author of extant works covering mathematics, astronomy, geography, chronology, and other fields. Little is known for certain of his life outside of his own writings, but he is considered the father of the exact and natural sciences in Armenia—the first Armenian mathematician, astronomer, and cosmographer.

A part of the Armenian Hellenizing School and one of the few secular scholars in medieval Armenia, Anania was educated primarily by Tychicus, in Trebizond. He composed science textbooks and the first known geographic work in classical Armenian (Ashkharhatsuyts), which provides detailed information about Greater Armenia, Persia and the Caucasus (Georgia and Caucasian Albania). (Full article...)
Image 8
Advanced Placement (AP) Statistics (also known as AP Stats) is a college-level high school statistics course offered in the United States through the College Board's Advanced Placement program. This course is equivalent to a one semester, non-calculus-based introductory college statistics course and is normally offered to sophomores, juniors and seniors in high school.

One of the College Board's more recent additions, the AP Statistics exam was first administered in May 1996 to supplement the AP program's math offerings, which had previously consisted of only AP Calculus AB and BC. In the United States, enrollment in AP Statistics classes has increased at a higher rate than in any other AP class. (Full article...)
Image 9
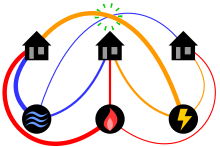
Diagram of the three utilities problem showing lines in a plane. Can each house be connected to each utility, with no connection lines crossing?

The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.

This puzzle can be formalized as a problem in topological graph theory by asking whether the complete bipartite graph $K_{3,3}$ , with vertices representing the houses and utilities and edges representing their connections, has a graph embedding in the plane. The impossibility of the puzzle corresponds to the fact that $K_{3,3}$ is not a planar graph. Multiple proofs of this impossibility are known, and form part of the proof of Kuratowski's theorem characterizing planar graphs by two forbidden subgraphs, one of which is $K_{3,3}$ . The question of minimizing the number of crossings in drawings of complete bipartite graphs is known as Turán's brick factory problem, and for $K_{3,3}$ the minimum number of crossings is one. (Full article...)
Image 10
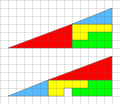
In this tiling of the plane by congruent squares, the green and violet squares meet edge-to-edge as do the blue and orange squares.

In geometry, Keller's conjecture is the conjecture that in any tiling of $n$ -dimensional Euclidean space by identical hypercubes, there are two hypercubes that share an entire $(n - 1)$ -dimensional face with each other. For instance, in any tiling of the plane by identical squares, some two squares must share an entire edge, as they do in the illustration.

This conjecture was introduced by Ott-Heinrich Keller (1930), after whom it is named. A breakthrough by Lagarias and Shor (1992) showed that it is false in ten or more dimensions, and after subsequent refinements, it is now known to be true in spaces of dimension at most seven and false in all higher dimensions. The proofs of these results use a reformulation of the problem in terms of the clique number of certain graphs now known as Keller graphs. (Full article...)
Image 11
Partition of a directed graph into a minimum feedback arc set (red dashed edges) and a maximum acyclic subgraph (blue solid edges)

In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at least one edge out of every cycle in the graph. Removing these edges from the graph breaks all of the cycles, producing an acyclic subgraph of the given graph, often called a directed acyclic graph. A feedback arc set with the fewest possible edges is a minimum feedback arc set and its removal leaves a maximum acyclic subgraph; weighted versions of these optimization problems are also used. If a feedback arc set is minimal, meaning that removing any edge from it produces a subset that is not a feedback arc set, then it has an additional property: reversing all of its edges, rather than removing them, produces a directed acyclic graph.

Feedback arc sets have applications in circuit analysis, chemical engineering, deadlock resolution, ranked voting, ranking competitors in sporting events, mathematical psychology, ethology, and graph drawing. Finding minimum feedback arc sets and maximum acyclic subgraphs is NP-hard; it can be solved exactly in exponential time, or in fixed-parameter tractable time. In polynomial time, the minimum feedback arc set can be approximated to within a polylogarithmic approximation ratio, and maximum acyclic subgraphs can be approximated to within a constant factor. Both are hard to approximate closer than some constant factor, an inapproximability result that can be strengthened under the unique games conjecture. For tournament graphs, the minimum feedback arc set can be approximated more accurately, and for planar graphs both problems can be solved exactly in polynomial time. (Full article...)
Image 12

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides.

The theorem can be written as an equation relating the lengths of the sides $a$ , $b$ and the hypotenuse $c$ , sometimes called the Pythagorean equation:
: $a^{2}+b^{2}=c^{2}.$
The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. (Full article...)

Did you know

... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
... that people in Madagascar perform algebra on tree seeds in order to tell the future?
... that owner Matthew Benham influenced both Brentford FC in the UK and FC Midtjylland in Denmark to use mathematical modelling to recruit undervalued football players?
... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
... that after Archimedes first defined convex curves, mathematicians lost interest in their analysis until the 19th century, more than two millennia later?
... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?

Did you know...

... that one can list every positive rational number without repetition by breadth-first traversal of the Calkin–Wilf tree?
... that the Hadwiger conjecture implies that the external surface of any three-dimensional convex body can be illuminated by only eight light sources, but the best proven bound is that 16 lights are sufficient?
... that an equitable coloring of a graph, in which the numbers of vertices of each color are as nearly equal as possible, may require far more colors than a graph coloring without this constraint?
... that no matter how biased a coin one uses, flipping a coin to determine whether each edge is present or absent in a countably infinite graph will always produce the same graph, the Rado graph?
...that it is possible to stack identical dominoes off the edge of a table to create an arbitrarily large overhang?
...that in Floyd's algorithm for cycle detection, the tortoise and hare move at very different speeds, but always finish at the same spot?
...that in graph theory, a pseudoforest can contain trees and pseudotrees, but cannot contain any butterflies, diamonds, handcuffs, or bicycles?

More did you know facts

Showing 7 items out of 75

Featured pictures

Image 1Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 2Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 3Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
$Image 4Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)$

Image 4Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 5Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 6Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 7Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 8Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 9Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 10Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
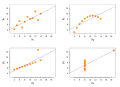
Image 11Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 12Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 13Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 14Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 15Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 16Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 17Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 18Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 19Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 20Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 21Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 22Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 23Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 24Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 25Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 26Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 27Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 28Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 29Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 30Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 31Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 32Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 33Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
Image 34Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals